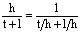
Cook et al. (1994) carried out pairwise choice tests on Papilio dardanus (race tibullus on the island of Pemba) by pinning out pairs of dead butterflies and counting the number of first approaches by males which were made to each butterfly. They used all three females morphs present (hippocoonides, trimeni, and lamborni), and also compared each of these with pinned-out males. In addition they compared hippocoonides and its model Amauris niavius, males with faded males, and trimeni and lamborni morphs with faded trimeni morphs. These comparisons are not used in the analysis, as the faded specimens and Amauris niavius were not compared in every possible combination.
The number of approaches recorded by Cook et al. for each comparison used in this analysis therefore is:
| Number of approaches to => When compared with | hippocoonides | trimeni | lamborni | male |
|---|---|---|---|---|
| hippocoonides | - | 11 | 7 | 11 |
| trimeni | 54 | - | 16 | 30 |
| lamborni | 42 | 40 | - | 43 |
| male | 41 | 48 | 26 | - |
Converting these to percentages gives:
| % of approaches to => When compared with | hippocoonides | trimeni | lamborni | male |
|---|---|---|---|---|
| hippocoonides | - | 16.9 | 14.3 | 21.2 |
| trimeni | 83.1 | - | 28.6 | 38.5 |
| lamborni | 85.7 | 71.4 | - | 62.3 |
| male | 78.8 | 61.5 | 37.7 | - |
For the data to be additive (i.e. for A:B and B:C to predict A:C), the ratio of A:B multiplied by the ratio of B:C multiplied by the ratio of A:C must equal 1. Therefore each combination of three morphs (including the male) can be tested for consistency with the data being additive:
hippocoonides:trimeni x trimeni:lamborni x hippocoonides:lamborni = 2.03
hippocoonides:trimeni x trimeni:male x hippocoonides:male = 2.1
hippocoonides:lamborni x lamborni:male x hippocoonides:male = 0.98
trimeni:lamborni x lamborni:male x trimeni:male = 0.94
From this analysis it can be seen that all the data, excluding that found for hippocoonides versus trimeni, can be taken to be additive. It is possible that the hippocoonides versus trimeni data is a statistical anomaly, or that this particular pairing causes a more complex effect on the males' preferences.
If the data as a whole is taken to represent the underlying preferences of the males, the expected preferences in the choice test between hippocoonides and trimeni can be calculated (by setting the top two equations above to one and substituting the values of the other ratios).
This gives the new percentage preferences for hippocoonides and trimeni to be 70.59% and 29.41% respectively.
Having taken the data to be additive, and calculated new values for the preferences of hippocoonides versus trimeni in order to make the data self-consistent, it is now possible to calculate the overall percentage preferences for each morph represented by the data.
The preference for hippocoonides (h) over lamborni (l) and trimeni (t) can be represented as:
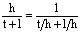 | Equation A5-1 |
Since t/h and l/h are known, the overall preference can be calculated. This can be done for each morph (and to check that these are correct, they should all add up to 100%).
This gives the percentage preferences for each morph to be:
hippocoonides: 63.16 trimeni: 26.32 lamborni: 10.53
If it is assumed that males only mate either once or twice (no broods from wild females reported by Ford (1936) indicate that a female had mated more than twice and so it seems a reasonable assumption that it is rare for males to mate more than twice), then the probability of a male choosing a hippocoonides (h) female in the mate choice experiments can be written as:
p(choosing h in experiment) = p(this is 1st mating) x p(choosing h in experiment on 1st mating)
+ p(this is 2nd mating) x p(choosing h in experiment on 2nd mating)
The probability that this is the first mating is taken to be 1-p(this is 2nd mating) since males are assumed to mate a maximum of two times.
If the males mate randomly on their first mating, as suggested by the results of Experiment 5-1, then the probability of mating with the hippocoonides female in the experiment is 1/3, as each morph was presented an equal number of times.
The probability that a male chooses hippocoonides on the second mating can be broken down:
p(choosing h on 2nd mating) = p(chose h on 1st mating) x p(choosing same morph)
+ p(chose t on 1st mating) x p(choosing h if chose t)
+ p(chose l on 1st mating) x p(choosing h if chose l)
Again, if the males mate randomly when naive, then the probability of choosing each morph on the first mating is equal to its proportion in the population (which was estimated by Cook et al.). If it is assumed that if a male does not choose the same morph on his second mating as on his first then he chooses randomly between the other two, then the p(choosing h if chose t) and p(choosing h if chose l) are both 0.5(1-p(choosing same morph).
Thus:
p(choosing h on 2nd mating) = p(h in population) x p(choosing same morph)
+ p(t in population) x 0.5(1- p(choosing same morph))
+ p(l in population) x 0.5(1- p(choosing same morph))
And overall:
p(choosing h in experiment) = [1- p(this is 2nd mating)] x 1/3
+ p(this is 2nd mating) x[p(h in population) x p(choosing same morph)
+ p(t in population) x 0.5(1- p(choosing same morph))
+ p(l in population) x 0.5(1- p(choosing same morph))]
Since the p(choosing h in the experiment) has been calculated from the data of Cook et al., and they also calculated the proportions of each morph in each population, this equation contains only two unknowns - the probability that the males mate twice and the probability of mating with the same morph twice. By substituting in the value for the probability of mating with the same morph on a second mating obtained from Experiment 5-2 it is possible to calculate the proportion of males which must have mated previously to give the results obtained by Cook et al. for each of the morphs.
| Parameter | Value | Source |
|---|---|---|
| proportion hippocoonides (h) | 0.8 | Cook et al. (1994) |
| proportion trimeni (t) | 0.16 | Cook et al. (1994) |
| proportion lamborni (l) | 0.04 | Cook et al. (1994) |
| probability choosing h in expt. | 0.63 | Calculated from Cook et al. (1994) |
| probability choosing t in expt. | 0.26 | Calculated from Cook et al. (1994) |
| probability choosing l in expt. | 0.1 | Calculated from Cook et al. (1994) |
| probability choosing same morph | 0.75 | Experiment 5-2 |
This substitution gives the proportion of males which must have already mated to give the results of Cook et al.'s choice tests for each morph:
hippocoonides: 102.26% trimeni: 64.78% lamborni: 124.4%
Giving an average of 97.14%.
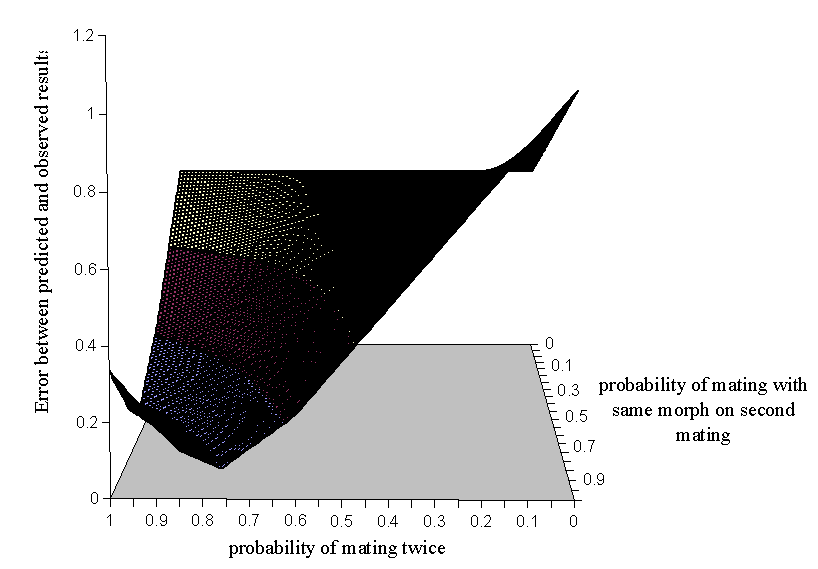
It is possible that the probability of choosing the same morph twice recorded in Experiment 5-2 is inaccurate, since this value is based on only 8 data points. However, if this value is treated as 'unknown' in the equations above, it is possible to solve the three equations simultaneously, to calculate the proportions of males expected to have mated already solely from the data of Cook et al. The easiest way in which to do this is to create a surface of the error between the results predicted by the three equations with varying values for the probability of mating twice and the probability of choosing the same morph twice, and to find the minimum value on the surface, representing the values of these two parameters which give the closest prediction to the observed results.
The surface produced is shown in Figure A5-1. From these results a minimum value for the error can be found, and it is where both the probability of mating twice and the probability of choosing the same morph on both those matings are 0.84.
Cook, S.E., Vernon, J.G., Bateson, M., Guilford, T. 1994. Mate choice in the polymorphic African swallowtail butterfly, Papilio dardanus: male-like females may avoid sexual harassment. Anim. Behav. 47: 389-397.
|
Please cite this thesis as: Freeman, ALJ; 1998; D.Phil thesis, Oxford University. |
E-mail to Alexandra Freeman Back to Table of Contents Back to Home Page |